Welcome Speech by Professor Chen-Ning Yang,
Chairman of Board of Adjudicators
Mr Shaw, Mr Chief Secretary, The honorable 2005 Shaw Prize Laureates, Ladies and Gentlemen:
On behalf of the Shaw Prize Council, I welcome all of you to this second annual ceremony. The Shaw Prize was established to encourage and to foster highest intellectual achievements essential for the welfare and progress of mankind. Thanks to the insightful deliberations and the diligent work of the 3 selection committees, the 2004 and 2005 Shaw Prize Laureates have won universal acclaim. The Shaw Prize has thus been referred to as the Nobel Prize of the East. We hope, in some future years, the Nobel Prize will be referred to as the Shaw Prize of the West.
Speech by Professor Frank H Shu,
Chairman of Astronomy Selection Committee
The discovery of extrasolar planets is one of the most dramatic and important findings in the history of Astronomy. For their roles in this development, Professor Michel Mayor of the University of Geneva and Professor Geoffrey Marcy of the University of California at Berkeley are awarded the Shaw Prize in Astronomy for 2005. Professor Mayor is being recognized for his discovery of the first planet around a normal star other than our own Sun. Professor Marcy is being recognized for his characterization of the masses and orbital properties of a large and statistically meaningful number of extrasolar planets and planetary systems.
The process of explaining the motions of the planets in our own Solar System spawned the Copernican Revolution. The later realization that stars are suns in their own right led to speculation that other planetary worlds might orbit distant suns. These speculations gained concrete foundation in 1995 when Mayor and Didier Queloz found a planet to orbit about the sunlike star, 51 Pegasi, with a 4-day period. The short period came as a shock because it meant that this giant planet, with about half of the mass of Jupiter, orbits its host star at a radius that is only 1% of the distance of Jupiter about our own Sun. Existing theories of planet formation held that giant planets should form in a rotating nebular disk surrounding a newly born star only beyond a so-called “frost line” where water vapor freezes and condenses out as solid ice. The exact location of the “frost line” at the time of giant planet formation is uncertain, but it should not have been much smaller than the present location of Jupiter, which is the innermost of the giant planets. The discovery of Mayor and Queloz electrified the field and spurred a huge increase in research activity on extrasolar planets, which has not abated to this day, ten years later.
Together with Paul Butler, Marcy quickly confirmed the reality of the 51 Pegasi planet using the method of precise Doppler measurement that he had developed for the purpose of extrasolar planet detection over many years. Seventy of the next 100 extrasolar planets discovered were found by his team. Many of these planets had distinctly non-circular orbits, in contrast with the orbits of known planets in our own Solar System. Several reside in systems where there is more than one giant planet, with multiple planets in a given system often having orbital periods that bear integer relationships to one another. As the observational sensitivity and the understanding of systematic errors steadily improve, planets with masses more like Saturn and Neptune are being found, instead of only the Jupiter-like bodies that characterized the initial discoveries. Significantly, there are no bodies that have masses appreciably in excess of 10 Jupiter masses. In a few cases, the orbital plane lies sufficiently edge-on to the observational line of sight that the giant planet transits in front of the host star, blocking out a small part of the star’s light, which allows an estimate of the radius of the transiting planet. A major surprise occurred in the latest such case where the combination of mass and radius implies that the planet has a dense rock-ice core that is seventy times the mass of the Earth, a much larger value than holds for any of the giant planets in our own solar system.
As the baseline for good orbital-period determinations passes the one decade mark, giant planets are being discovered with orbital distances from their host stars more akin to the case of our own Solar System. The stage is now being set for answering one of the most intriguing questions ever posed in science: how typical or atypical is our own Solar System? For moving this question from the dreamy realm of philosophical speculation to the concrete field of empirical fact, Michel Mayor and Geoff Marcy are justly honored tonight with the award of the Shaw Prize in Astronomy for 2005.
Speech by Professor Arthur K C Li,
Chairman of Life Science and Medicine Selection Committee
Cells in the human body communicate with each other and their activities are regulated. Sir Michael Berridge’s discovery of calcium signaling in the regulation of cellular activity has truly revolutionized the fields of life science and medicine. How various factors increase calcium mobilization and how calcium controls cellular activity has widely expanded the areas of cell and molecular biology. This has led to the development of new treatment of heart disease to the improvement of learning and memory. These discoveries represent one of the most important cell signaling pathways in biology and have changed forever the way we think about prevention and treatment of disease.
Cellular communication occurs through chemical signals such as hormones, neurotransmitters and nitric oxide, which act via specific receptors or receptive molecules and are linked to diverse intracellular and extracellular signaling pathways. The signaling system discovered by Berridge is of fundamental importance in regulating diverse cellular processes such as muscle contraction, cell growth and differentiation, secretion, fertilization, synaptic plasticity and information processing. In the early 1970s, Berridge published a series of papers demonstrating that calcium and cyclic AMP functioned as separate and distinct signaling pathways that interacted with each other. Then, he published a series of papers leading to his discovery that IP3 was the messenger linking surface receptors to the mobilization of internal calcium (Biochem. J. 212: 849-858, 1983). Berridge’s discovery that IP3 functioned as a messenger molecule started an avalanche of work on the metabolism of inositol phosphates and on the calcium mobilizing action of IP3.
Berridge’s work on the spatial and temporal aspects of calcium signaling has laid the foundation for our current understanding of how information is encoded and decoded in the nervous system and in the cardiovascular system. His discoveries have impacted on widely diverse areas of biology and medicine such as memory and learning, cell growth, fertilization, myocardial contraction, glandular secretion and the mechanism of action of lithium.
The impact of these discoveries on the betterment of mankind has been astounding. The seminal contributions made by Berridge on IP3 and its role in calcium signaling made it possible to unravel numerous signaling pathways in biology and to show the links between such pathways and the central role played by calcium. The work of Berridge has had many practical consequences, not only in establishing a basis for our understanding of how cells are regulated but also in providing novel insights into a variety of human diseases.
Speech by Professor Wentsun Wu,
Chairman of Mathematical Sciences Selection Committee
I feel a great honour in giving the Presentation Lecture for 2005 Laureate Professor Andrew WILES in Mathematical Sciences owing to his outstanding achievements in Number Theory and other domains of mathematics, particularly the monumental complete settlement of 356year-old FERMAT LAST THEOREM.
The FERMAT LAST THEOREM or FLT for short, had a long fascinating history. It asks whether there are positive integer solutions in (x,y,z) of the equation
| xn + yn = zn | (In) |
for integer exponent n > 2. The case n = 2 is well-known already in remote antiquity. In fact, let x, y, z be the lengths of the two sides and the hypothenus of a right-angled triangle or a Gou-Gu Form in ancient China’s terminology. Then equation (I2) is the famous Pythagorean equation or the Gou-Gu Theorem in China’s antiquity. It is also well-known that the equation (I2) has positive integer solutions (x,y,z) = (3,4,5), (5,12,13), etc., see the accompanying figure below:
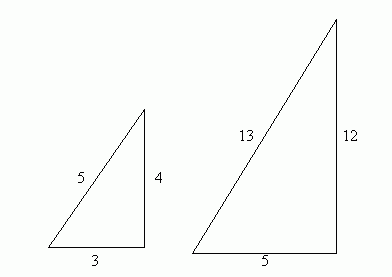
In fact, in the Chinese ancient classic 《Nine Chapters of Arithmetic》 more than 2000 years before it is already described that the whole set of possible positive integer solutions of (I2), with Gou, Gu, Xuan as the lengths of two sides and the hypothenus of a right-angled triangle or a Gou-Gu Form, is given by
| x : y : z = Gou : Gu : Xuan = p 2 – q 2 : 2pq : p 2 + q 2 | (II) |
| for integers p, q. |
Besides (x,y,z) = (3,4,5), (5,12,13) the 《Nine Chapters》 also listed the solutions (7,24,25), (8,15,17), (20,21,29), (48,55,73), (60,91,109), (20,99,101) corresponding to the case (p, q) = (2, 1), (3, 2), (4, 2), (5, 3), (7, 3), (11, 5), (13, 7), (11, 9), respectively in the Eq. (II). Moreover, in the 《Annotations to Nine Chapters》 of scholar LIU Hui of 3c A.D. LIU had given a rigorous proof of (II).
While the case n = 2 is elementary and understandable by school boys, the case n > 2 is entirely different. In year 1637 the French jurist Piere de Fermat, as an amateur in mathematics, announced that for n > 2 the equation (In) had no positive integer solutions at all. Fermat himself had proved the case n = 4 and in 17th century the great mathematician L. Euler had proved FLT for n = 3,5. However, the “lost” or actually “non-existant” proof of Fermat had puzzled mathematicians since that time. To “rediscover” or to “discover” a proof of FLT had attracted the greatest mathematical minds of the later years and centuries but resulted always in failure. However, in spite of these failures their efforts had brought out the fruits of giving impetus to some important mathematics disciplines and even naissance to new ones. Moreover, some new ideas introduced, the notion of ideals for example, had henceforth penetrated into the whole domain of mathematics and became henceforth indispensable tools for mathematical researches.
By the late 20th century it had been shown that FLT was known to be true for an infinity of exponents n and is true for 3 < n < 4,000,000. However, it is yet infinitely far from the ultimate goal: FLT should be true for all n > 3.
It comes now the final astonishing result of A Wiles. Around ninetieth of last century, A.Wiles had already become reknown to mathematics circle owing to his dramatic achievements on many delicate problems in number theory. In the long run A.Wiles announced in year 1993 at the end of a series of lectures in Cambridge that the FLT had been thus proved. This not only completely solves the 356year-old problem but the method involved will influence the development of mathematics as a whole. In particular it had a deep impact to the important subject of algebraic geometry.
The announcement causes a thunder-like shock to the whole of mathematical society and a wide range of amateurs. The whole paper appeared in Annals of Mathematics, vol141, (1995), of length about 110 pages.
It is for such Olympian accomplishments that we have the honour of declaring that the 2005 Shaw Prize in mathematical sciences is offered to
Professor Andrew WILES !!!
