The attractive force of gravity is responsible for the formation of bound structures over a wide range of scales, from planets to clusters of galaxies. Unbalanced, gravity would cause matter to collapse into black holes. Fortunately, the concentration of mass by gravity is impeded, at least temporarily, by the requirement that the contracting material rid itself of excess energy and angular momentum. Bulk kinetic energy can be converted into heat and radiated away but angular momentum is less readily disposed of. Consequently, contracting material often assumes the form of a differentially rotating disk. Familiar examples include Saturn’s rings and spiral galaxies. Nascent stars grow by accreting mass from disks that live several million years. The coplanar orbits of the solar system planets and multi-planet systems around other stars are vestiges of these disks.
More exotic accretion disks are found around compact objects such as white dwarfs, neutron stars and black holes. These systems shine by radiating gravitational potential energy released as mass spirals inward. For fluid to spiral in, its angular momentum must be transported out, but how this happens was for long a mystery. For decades, it was speculated that accretion disks were unstable and that the accretion torque arises from turbulent stresses. However, analytic analyses and numerical simulations consistently failed to identify any appropriate instability. In 1991 Balbus & Hawley announced an elegant solution to this longstanding problem. They demonstrated that even a weak seed magnetic field is sufficient to unleash a powerful instability, the magnetorotational instability (MRI), that both creates and sustains turbulence while also amplifying the magnetic field.
The beauty and simplicity of the MRI is neatly captured graphically. Data for the plots shown below (Fig. 1) were obtained by solving Newton’s equations of motion for two identical particles revolving counterclockwise around a spherical central mass. In the upper sequence the particles move independently on circular coplanar orbits. As discovered by Kepler and later explained by Newton, the orbital period increases as radius raised to the 3/2 power. This accounts for the growing lead in longitude of the inner (green) particle with respect to the outer (red) one. The separation of the particles increases by about a factor of five in a single orbital period. In the lower sequence, the particles are connected by an elastic tether whose tension increases in proportion to its length. Although the particles start out on circular orbits, deviations soon become apparent. By the end of the sequence both their separation and the tension in the tether have increased more than tenfold. Comparison of the upper and lower sequences reveals a remarkable fact. Two particles separate more rapidly when gently pulled towards each other by the tether than they do when moving independently. This is a consequence of the seemingly obstinate behavior of an orbiting body. Gently pulled forward (backward), it moves onto an orbit of larger (smaller) radius where it orbits more slowly (rapidly).
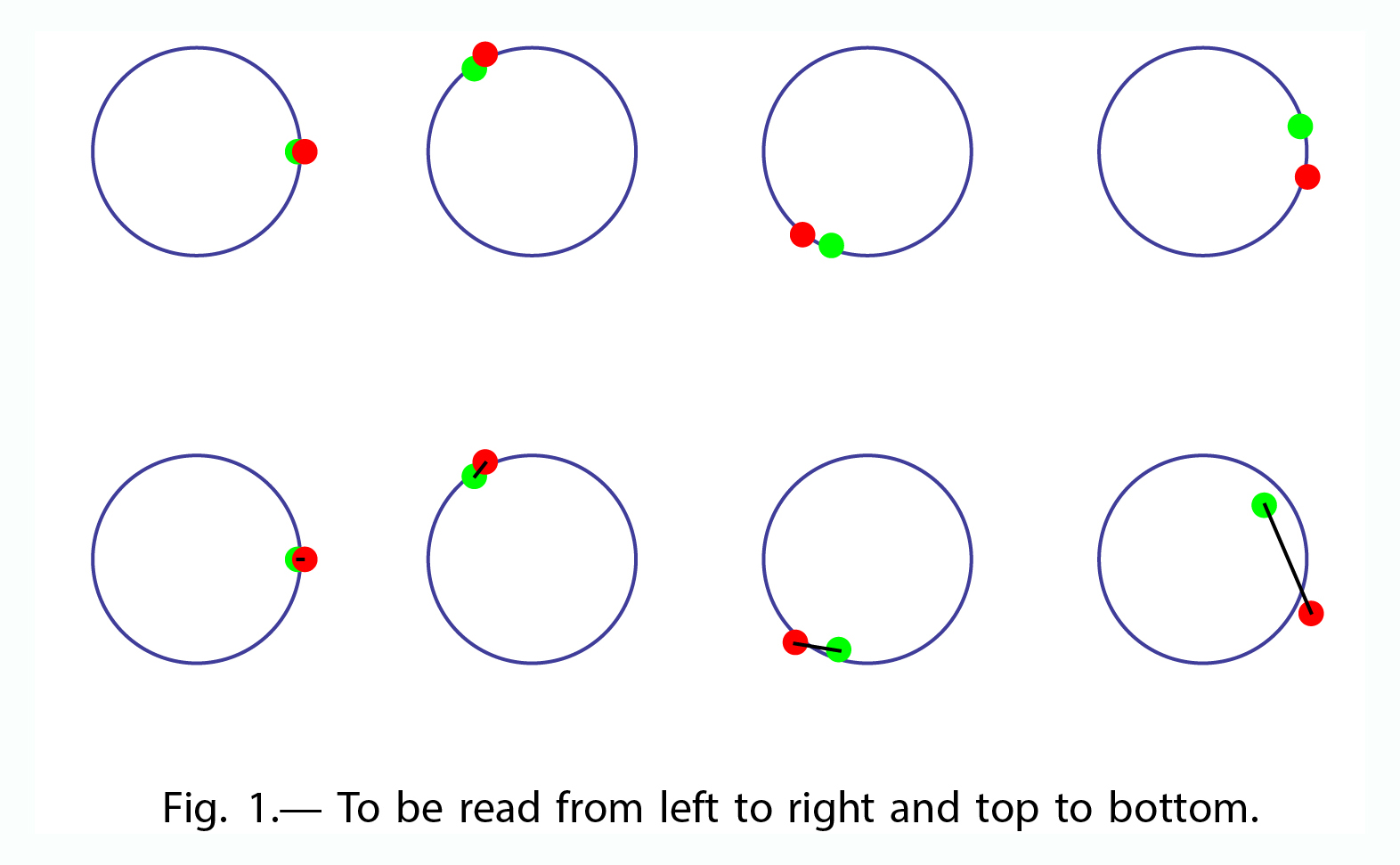
The tether transfers angular momentum and energy from the inner to the outer particle. The total angular momentum carried by the two particles remains unchanged. However, their total energy decreases with the deficit stored as elastic energy in the tether. It is important that the behavior of the particles linked by the tether is an instability. The rate at which the inner particle spirals inward and the outer outward is proportional to the tether’s tension. Moreover, the rate at which the tension increases depends upon the rate at which the particles separate. No matter how small the initial tension is set, both the separation of the particles and the magnitude of the tension grow exponentially.
How does this simple example relate to the MRI? Given sufficient electrical conductivity, magnetic field lines couple fluid elements they link and provide a tension which grows as they stretch. A key point is that the MRI amplifies weak magnetic fields. This is the crucial ingredient of a dynamo. A full treatment of the MRI requires large scale numerical simulations. In place of our simple two particle system, imagine many pairs of particles connected by tethers. As they move the tethers stretch, break and reconnect. Viewed this way, perhaps it is not surprising that a fluid undergoing the MRI exhibits a complicated flow called turbulence.
Astronomy Selection Committee
The Shaw Prize
23 September 2013 Hong Kong
